A (Somewhat Failed) Experiment in Latent Reasoning with LLMs
Introduction
The current generation of large language models (LLMs) demonstrate strong performance in reasoing tasks such as grade-school mathematics, driven in part by test-time scaling. Despite this progress, their solutions often involve unnecessarily long natural-language chains of thought, leading to substantial number of token generation and high computational cost. Moreover, human reasoning is largely abstract and not confined to natural language. Recent findings by Yong et al.1 also indicate that strong reasoning performance in one language does not necessarily transfer to others. These observations motivate the question: can LLMs perform their internal reasoning in a latent space, without producing explicit natural-language traces? This work explores one such direction by inducing models to reason using non-semantic thought tokens rather than natural text.
Experiments
The main idea is to augment the model’s vocabulary with a set of newly introduced ‘thought tokens’, whose embeddings were initialized randomly and devoid of any inherent meaning at first, and constrain the model to perform all intermediate reasoning using only these tokens. Given a question, the input takes the form <bos_token>{question}, and the desired model output is: <thought_a><thought_b>…<thought_n>#####{answer}<eos_token>.
Training proceeds in two stages. At first, we go through a supervised fine-tuning (SFT) stage, where we sample 15,000 question–answer pairs from GSM8K-aug dataset (Deng et al.2) and append a sequence of 10 randomly selected thought tokens after each question. The loss is the negative log-likelihood over the answer portion, where the tokens from the question and thought portions are masked out. This stage teaches the model to follow the prescribed output format and to place the answer immediately after the ##### delimiter.
Next, we perform reinforcement learning on a smaller subset of the GSM8K train set (Cobbe et al.3). For each question, we generate multiple candidate answers, and then use the Dr. GRPO variant (Liu et al.4) of the Group Relative Policy Optimization (GRPO) algorithm (Shao et al.5) to maximize the proportion of correct answers across rollouts. To ensure the model’s adherence to the latent-token reasoning constraint during RL, we also mask out the logits associated with all non-thought tokens, renormalize the resulting distribution, and sample exclusively from the thought-token subspace when generating the intermediate sequences. After producing the fixed-length thought sequence, we append the ##### token manually and allow the model to generate the final answer. I also used an active sampling strategy (Ettinger et al.6) to avoid selecting problems that are either trivial or overly difficult, both of which would yield near-zero advantages and consequently no effective gradient updates. A small held-out portion of the GSM8K test set is used to monitor performance throughout the RL phase. Due to compute constraints, I could use only 4 questions per rollout. At first 8 answers per question are generated and then a subset of 6 are selected such that there is at least one correct answer for each question in the batch. Any question where all or none of the model generated answers matches with the ground truth answer are discarded from the batch and another question is sampled until the sample size reaches 4.
All experiments were conducted using LLaMA-3.2 3B and Qwen-3 1.7B models. A set of 100 new tokens were added to extend the original vocabulary and each model was restricted to generate exactly 10 thought tokens per question.
Results
During training, we keep track of two metrics: mean accuracy (the ratio of correct answers to total number of generated answers) and pass@k, where we generate eight answers per question and set \(k=5\). For both LLaMA and Qwen models, we perform 1000 update steps. Both metrics see an increasing trend over the course of training, although progress is noisy and relatively slow. Despite these upward trends, the comparative results are less encouraging.
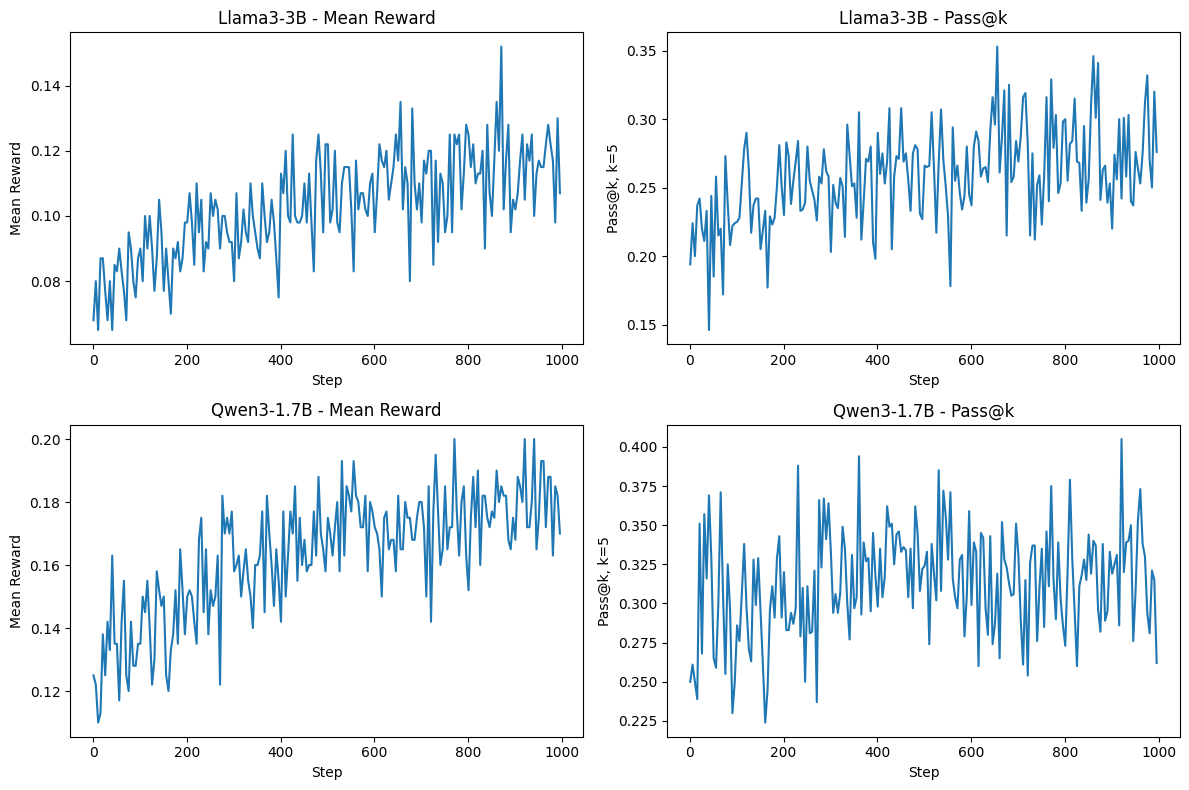
I evaluated the base model, the SFT model, and the final RL-trained model on the full GSM8K test set under four conditions. For the base model, I provided the question alone and ask the model to produce an answer without explanations. For the SFT model, I appended ten randomly sampled thought tokens to each question, added the ##### delimiter, and allowed the model to generate the final answer. For evaluating the final RL model, I used the question as the initial prompt, sampled 10 thought tokens by masking out all non-thought tokens and renormalizing the distribution, and then appended the delimiter before generating the answer. To determine whether the model’s own generated thought tokens matter, I additionally evaluated the RL model in an SFT-style setting where I instead prepended ten randomly selected thought tokens before #####, bypassing the model’s internal reasoning tokens entirely.
Although both SFT and RL improve accuracy and pass@k for LLaMA and Qwen relative to their respective base models, we observe no statistically significant difference between the RL model using its generated thought tokens and the same model using random thought tokens. The metrics for all four evaluation settings for both model families are summarized in the table below.
| Model Setting | Qwen 3 1.7B | LLaMA 3.2 3B | ||
|---|---|---|---|---|
| Mean Accuracy | Pass@k | Mean Accuracy | Pass@k | |
| Base Model | 0.0565 ± 0.0060 | 0.1270 ± 0.0172 | 0.0585 ± 0.0028 | 0.1717 ± 0.0080 |
| SFT | 0.1482 ± 0.0017 | 0.3104 ± 0.0051 | 0.0882 ± 0.0011 | 0.2430 ± 0.0058 |
| RL w/ Random Thoughts | 0.1938 ± 0.0022 | 0.3223 ± 0.0073 | 0.1199 ± 0.0021 | 0.2775 ± 0.0070 |
| RL | 0.1929 ± 0.0024 | 0.3289 ± 0.0075 | 0.1173 ± 0.0026 | 0.2692 ± 0.0056 |
Conclusion
Although I was hoping that the RL phase will force the LLM to use the thought tokens ‘intelligently’, in reality their inclusion did not improve the model performance. I suspect that, during the SFT phase the thought tokens were inserted randomly because of which the model learnt that they are irrelevant and in the RL training phase, the sparse and delayed reward signal could not help much. I also looked at the probability distribution over the set thought tokens in a few sequences and found all of them to be pretty much uniformly random. It would be interesting to see if there is a way to teach the model to always output a non-uniform probability distribution over these thought tokens (e.g., maybe in addition to maximizing accuracy in the RL phase, we can add the sum of negative entropy of the distributions over the thought tokens as an auxiliary objective). Overall, the findings indicate that forcing the model to use thought tokens is not enough; without a meaningful learning signal, RL cannot endow those tokens with useful semantics.
The code for this work is available here.
References
-
Yong, Zheng-Xin; Adilazuarda, M. Farid; Mansurov, Jonibek; Zhang, Ruochen; Muennighoff, Niklas; Eickhoff, Carsten; Winata, Genta Indra; Kreutzer, Julia; Bach, Stephen H.; Aji, Alham Fikri. Crosslingual Reasoning through Test-Time Scaling. 2025.
https://arxiv.org/abs/2505.05408 ↩ -
Deng, Yuntian; Prasad, Kiran; Fernandez, Roland; Smolensky, Paul; Chaudhary, Vishrav; Shieber, Stuart. Implicit Chain of Thought Reasoning via Knowledge Distillation. 2023.
https://arxiv.org/abs/2311.01460 ↩ -
Cobbe, Karl; Kosaraju, Vineet; Bavarian, Mohammad; Chen, Mark; Jun, Heewoo; Kaiser, Lukasz; Plappert, Matthias; Tworek, Jerry; Hilton, Jacob; Nakano, Reiichiro; Hesse, Christopher; Schulman, John. Training Verifiers to Solve Math Word Problems. 2021.
https://arxiv.org/abs/2110.14168 ↩ -
Liu, Zichen; Chen, Changyu; Li, Wenjun; Qi, Penghui; Pang, Tianyu; Du, Chao; Lee, Wee Sun; Lin, Min. Understanding R1-Zero-Like Training: A Critical Perspective. 2025.
https://arxiv.org/abs/2503.20783 ↩ -
Shao, Zhihong; Wang, Peiyi; Zhu, Qihao; Xu, Runxin; Song, Junxiao; Bi, Xiao; Zhang, Haowei; Zhang, Mingchuan; Li, Y. K.; Wu, Y.; Guo, Daya. DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models. 2024.
https://arxiv.org/abs/2402.03300 ↩ -
Ettinger, Allyson, et al. Olmo 3 Technical Report. 2025.
Olmo 3 Technical Report ↩